AE 12: Logistic regression introduction

Published

October 30, 2023

Important

Go to the course GitHub organization and locate your ae-12 repo to get started.

Render, commit, and push your responses to GitHub by the end of class. The responses are due in your GitHub repo no later than Thursday, November 2 at 11:59pm.

Packages

library(tidyverse)
library(tidymodels)
library(knitr)

heart_disease <- read_csv("data/framingham.csv") |>
  select(totChol, TenYearCHD) |>
  drop_na() |>
  mutate(high_risk = as.factor(TenYearCHD)) |>
  select(totChol, high_risk)

Data: Framingham study

This data set is from an ongoing cardiovascular study on residents of the town of Framingham, Massachusetts. We want to use the total cholesterol to predict if a randomly selected adult is high risk for heart disease in the next 10 years.

high_risk:
- 1: High risk of having heart disease in next 10 years
- 0: Not high risk of having heart disease in next 10 years
totChol: total cholesterol (mg/dL)

Outcome: `high_risk`

ggplot(data = heart_disease, aes(x = high_risk)) + 
  geom_bar() + 
  scale_x_discrete(labels = c("1" = "High risk", "0" = "Low risk")) +
  labs(
    title = "Distribution of 10-year risk of heart disease", 
    x = NULL)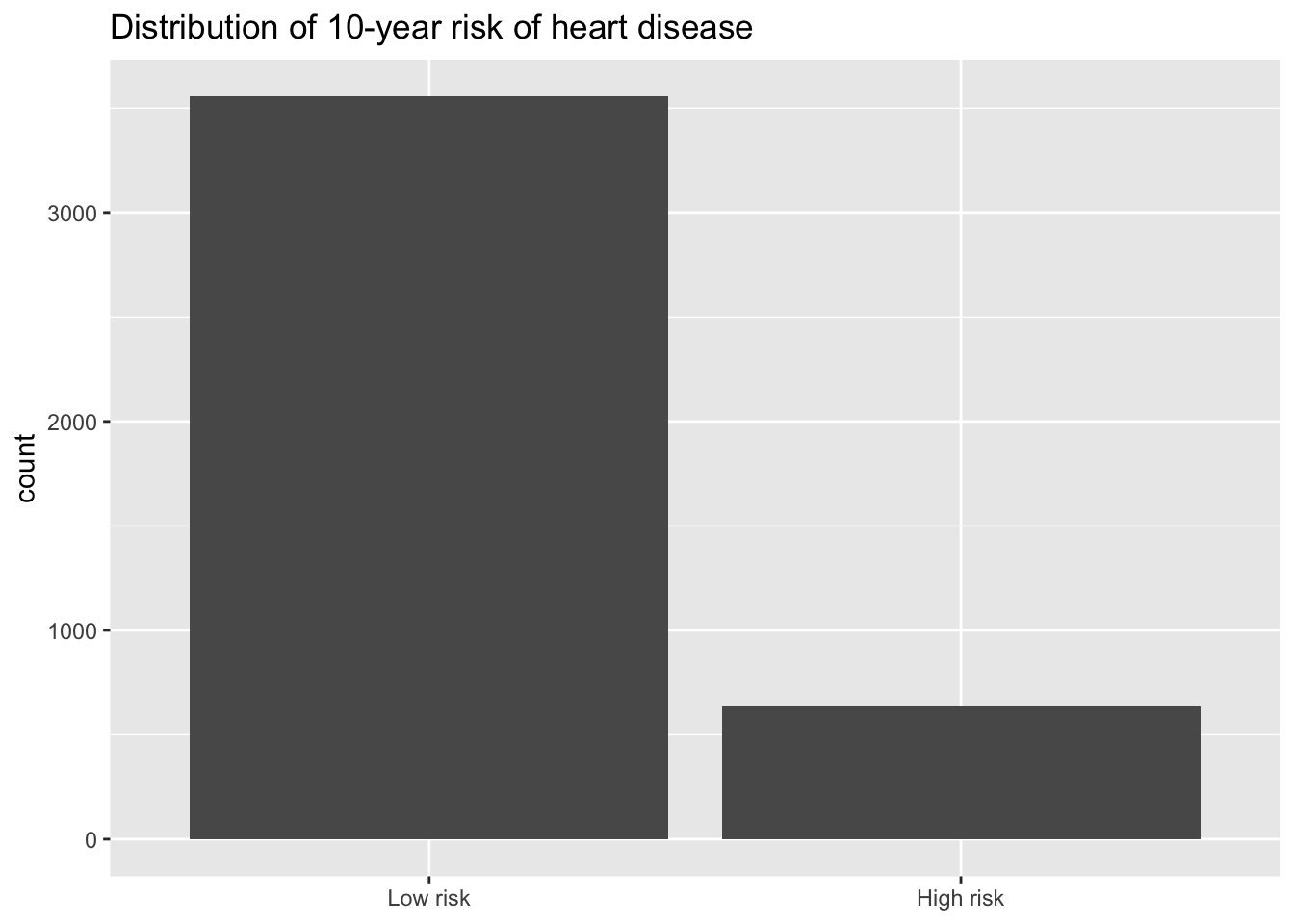

heart_disease |>
  count(high_risk)

# A tibble: 2 × 2
  high_risk     n
  <fct>     <int>
1 0          3555
2 1           635

Calculating probability and odds

What is the probability a randomly selected person in the study is not high risk for heart disease in the next 10 years?
What are the odds a randomly selected person in the study is not high risk for heart disease in the next 10 years?

Logistic regression model

Fit a logistic regression model to understand the relationship between total cholesterol and risk for heart disease.

Let \(\pi\) be the probability an adult is high risk of heart disease. The statistical model is

\[\log\Big(\frac{\pi_i}{1-\pi_i}\Big) = \beta_0 + \beta_1 TotChol_i\]

heart_disease_fit <- logistic_reg() |>
  set_engine("glm") |>
  fit(high_risk ~ totChol, data = heart_disease, family = "binomial")

tidy(heart_disease_fit) |> kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	-2.894	0.230	-12.607	0
totChol	0.005	0.001	5.268	0

Write the regression equation. Round to 3 digits.

Calculating log-odds, odds and probabilities

Based on the model, if a randomly selected person has a total cholesterol of 250 mg/dL,

What are the log-odds they are high risk for heart disease in the next 10 years?
What are the odds they are high risk for heart disease in the next 10 years?
What is the probability they are high risk for heart disease in the next 10 years? Use the odds to calculate your answer.

Comparing observations

Suppose a person’s cholesterol changes from 250 mg/dL to 200 mg/dL.

How do you expect the log-odds that this person is high risk for heart disease in the next 10 years to change?
How do you expect the odds that this person is high risk for heart disease in the next 10 years to change?

Submission