AE 08: Exam 01 Review

Published

October 2, 2023

Important

Go to the course GitHub organization and locate your ae-08 repo to get started.

Render, commit, and push your responses to GitHub by the end of class. The responses are due in your GitHub repo no later than Thursday, October 5 at 11:59pm.

Packages

library(tidyverse)
library(tidymodels)
library(knitr)
library(patchwork)

Restaurant tips

What factors are associated with the amount customers tip at a restaurant? To answer this question, we will use data collected in 2011 by a student at St. Olaf who worked at a local restaurant.1

The variables we’ll focus on for this analysis are

  • Tip: amount of the tip
  • Party: number of people in the party

View the data set to see the remaining variables.

tips <- read_csv("data/tip-data.csv")

Exploratory data analysis

p1 <- ggplot(data = tips, aes(x = Tip)) + 
  geom_histogram(color = "white", binwidth = 2) +
  labs(x = "Tips ($)",
       title = "Tips at local restaurant")

p2 <- ggplot(data = tips, aes(x = Party)) + 
  geom_histogram(color = "white") +
  labs(x = "Party",
       title = "Number of diners in party") +
  xlim(c(0, 7))

p3 <- ggplot(data = tips, aes(x = Party, y = Tip)) + 
  geom_jitter() + 
  labs(x = "Number of diners in party", 
       y = "Tips ($)",
       title = "Tips vs. Party")

(p1 + p2) / p3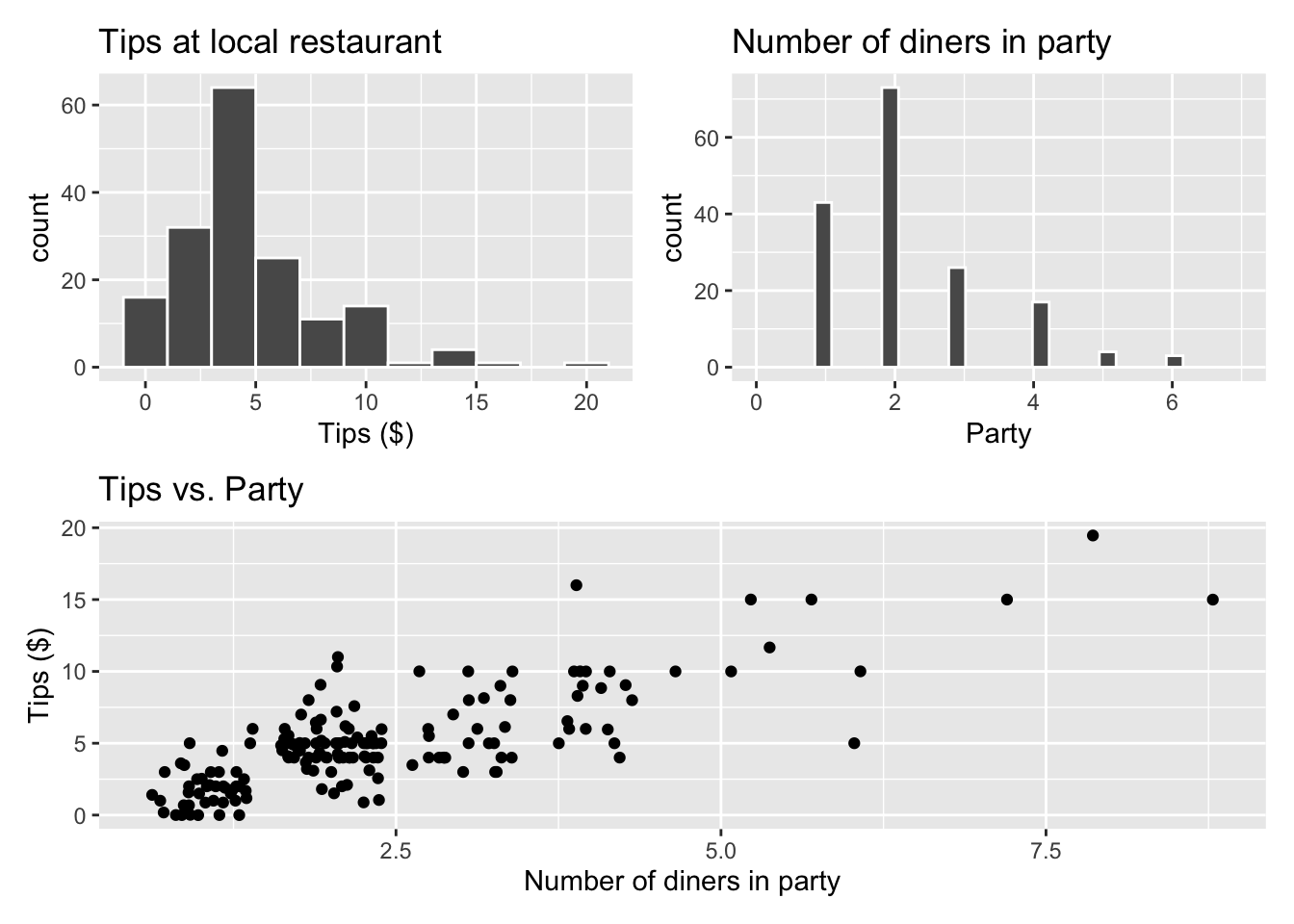

The goal is to fit a model that uses the number of diners in the party to understand variability in the tips.

Exercise 1

Write the statistical model.

[add answer here]

Exercise 2

The regression output with 90% confidence intervals for the coefficients is shown below.

tips_fit <- linear_reg() |>
  fit(Tip ~ Party, data = tips)

tidy(tips_fit, conf.int = TRUE, conf.level = 0.9) |>
  kable(digits = 3)
term estimate std.error statistic p.value conf.low conf.high
(Intercept) 0.383 0.321 1.195 0.234 -0.147 0.913
Party 1.957 0.118 16.553 0.000 1.761 2.152 
glance(tips_fit)$sigma
[1] 2.082824

Write the regression equation.

[add answer here]

Exercise 3

The regression standard error is 2.083. Write the definition of this value in the context of the data.

[add answer here]

Exercise 4

tips_aug <- augment(tips_fit$fit)

rsq(tips_aug, truth = Tip, estimate = .fitted)
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rsq     standard       0.621
rmse(tips_aug, truth = Tip, estimate = .fitted)
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard        2.07

  • Interpret \(R^2\) in the context of the data.

  • Interpret RMSE in the context of the data.

  • Based on these values, do you think the model is a good fit for the data? Why or why not?

[add answer here]

Exercise 5

The following code can be used to create a bootstrap distribution for the slope (and the intercept, though we’ll focus primarily on the slope in our inference). Describe what each line of code does, supplemented by any visualizations that might help with your description.

set.seed(1234)

1boot_dist <- tips |>
2  specify(Tip ~ Party) |>
3  generate(reps = 100, type = "bootstrap") |>
  fit()
1
___________
2
___________
3
___________

Exercise 6

Use the bootstrap distribution created in the previous exercise, boot_dist, to construct a 90% confidence interval for the slope. Interpret the interval in the context of the data.

# add your code here

Conduct a hypothesis test using permutation with 100 reps. State the hypotheses in words and mathematical notation. Also include a visualization of the null distribution of the slope with the observed slope marked as a vertical line.

Use \(\alpha = 0.1\) as the decision-making threshold for rejecting or failing to reject the null hypothesis.

set.seed(1234)
# add your code here

Exercise 7

Check the relevant conditions for Exercises 5 and 6. Are there any violations in conditions that make you reconsider your inferential findings?

# add your code here

Exercise 8

Now repeat Exercises 5 and 6 using approaches based on mathematical models. You can reference output from previous exercises and/or write new code as needed.

[add answer here]

Exercise 9

Note

Check the relevant conditions for Exercise 8. Are there any violations in conditions that make you reconsider your inferential findings? You can reference previous graphs / conditions and add any new code as needed.

# add your code here

Exercise 10

  • Based on your model, predict the tip for a party of 4.

  • Suppose you’re asked to construct a 95% confidence and a 95% prediction interval for your finding in the previous exercise. Which one would you expect to be wider and why? In your answer clearly state the difference between these intervals.

  • Now construct the intervals and comment on whether your guess is confirmed.

# add your code here

To submit the AE:

Important
  • Render the document to produce the PDF with all of your work from today’s class.
  • Push all your work to your ae-08 repo on GitHub. (You do not submit AEs on Gradescope).

Footnotes

  1. Dahlquist, Samantha, and Jin Dong. 2011. “The Effects of Credit Cards on Tipping.” Project for Statistics 212-Statistics for the Sciences, St. Olaf College.↩︎