The big picture

Analyzing multivariable relationships + Reproducibility

Prof. Maria Tackett

Aug 30, 2023

Announcements

  • Resources for extra R review

    • Learn R: An interactive introduction to data analysis R (focus on Chapters 4 - 6)

    • Duke Library Center for Data and Visualization Sciences workshops

      • R for Lunch: data wrangling with dplyr (Fri, Sep 1, 12:30 - 1:30)

      • R for Lunch: visualization with ggplot2 (Fri, Sep 8, 12:30 - 1:30)

      • See the CDVS website for more information and to register.

  • Last day of in-person work for this class is Dec 7
  • Lecture recordings request policy
  • Readings for next week will be posted later this week

Questions from last class?

Topics

  • Data analysis life cycle
  • Reproducible data analysis
  • Analyzing multivariable relationships

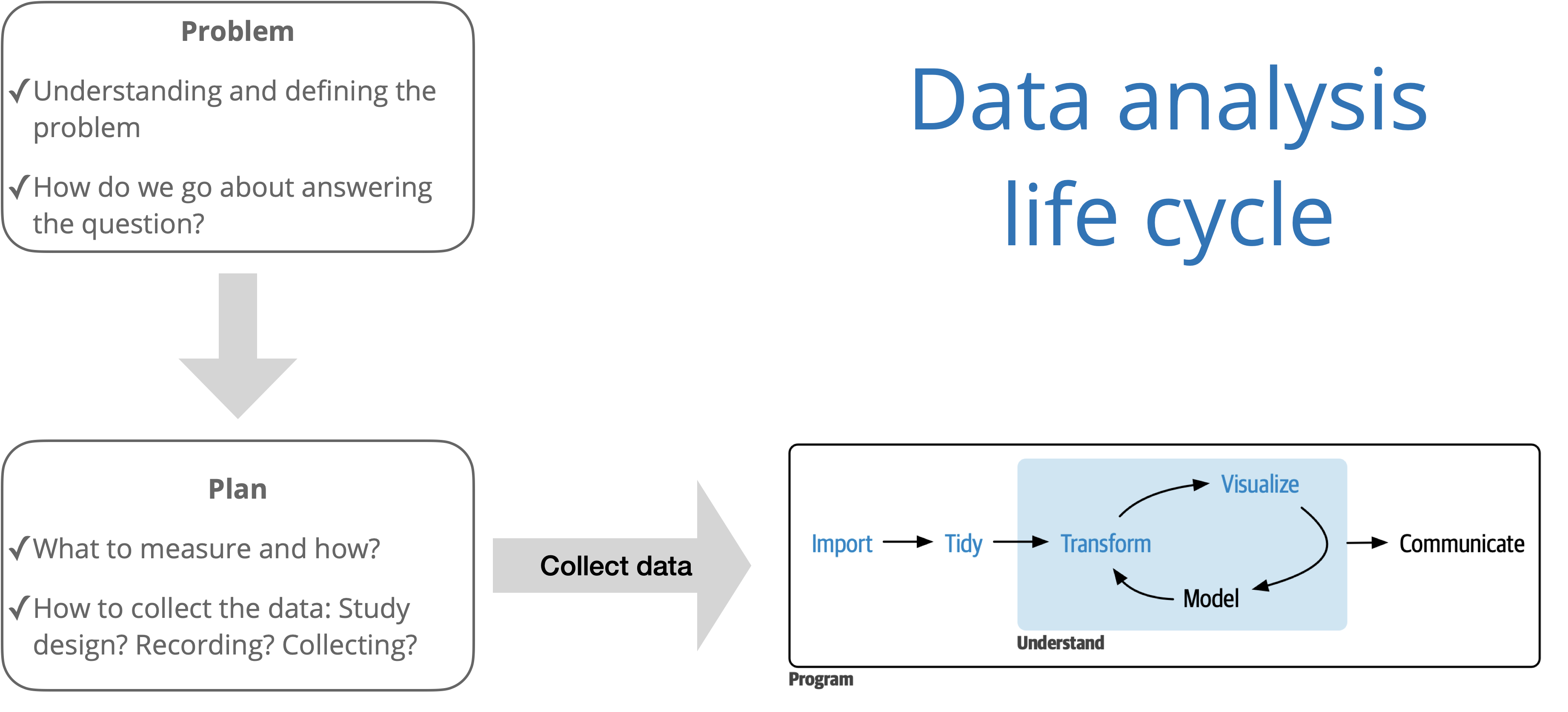
Source: R for Data Science with additions from The Art of Statistics: How to Learn from Data.

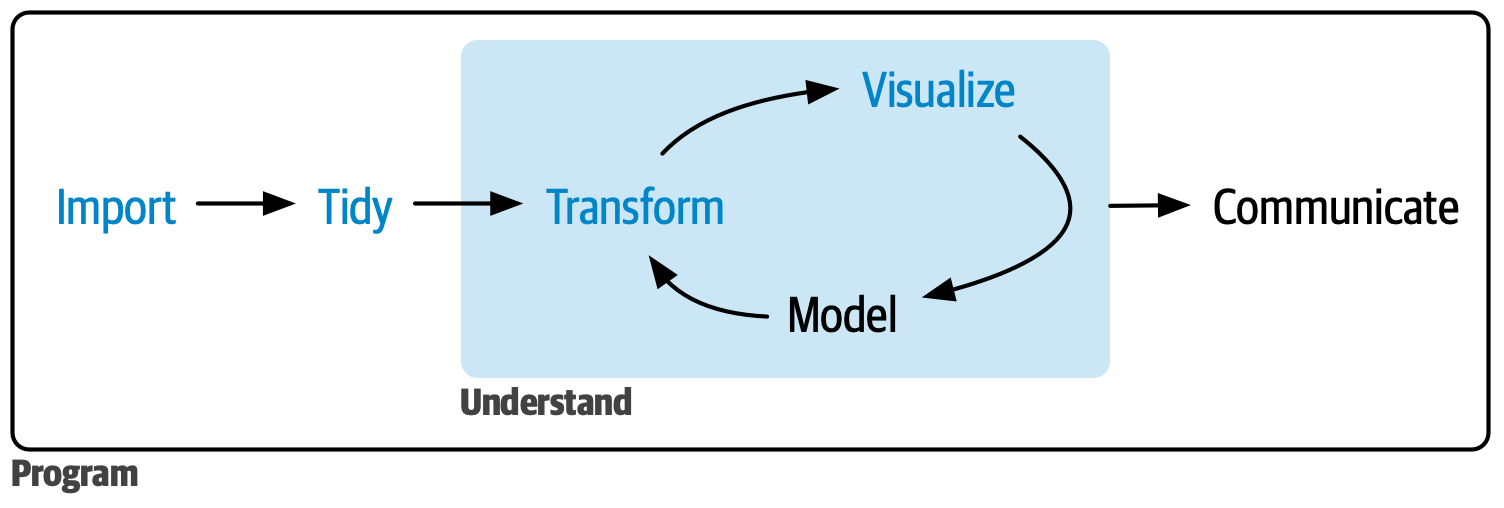
Source:R for Data Science

Reproducibility

Reproducibility checklist

What does it mean for an analysis to be reproducible?

Near term goals:

✔️ Can the tables and figures be exactly reproduced from the code and data?

✔️ Does the code actually do what you think it does?

✔️ In addition to what was done, is it clear why it was done?

Long term goals:

✔️ Can the code be used for other data?

✔️ Can you extend the code to do other things?

Why is reproducibility important?

When things go wrong

Reproducibility error Consequence Source(s)
Limitations in Excel data formats Loss of 16,000 COVID case records in the UK (Kelion 2020)
Automatic formatting in Excel Important genes disregarded in scientific studies (Ziemann, Eren, and El-Osta 2016)
Deletion of a cell caused rows to shift Mix-up of which patient group received the treatment (Wallensteen et al. 2018)
Using binary instead of explanatory labels Mix-up of the intervention with the control group (Aboumatar and Wise 2019)
Using the same notation for missing data and zero values Paper retraction (Whitehouse et al. 2021)
Incorrectly copying data in a spreadsheet Delay in the opening of a hospital (Picken 2020)

Source: Ostblom and Timbers (2022)

Toolkit

  • Scriptability \(\rightarrow\) R

  • Literate programming (code, narrative, output in one place) \(\rightarrow\) Quarto

  • Version control \(\rightarrow\) Git / GitHub

Note

You will start using these computing tools in Lab 01.

R and RStudio

  • R is a statistical programming language

  • RStudio is a convenient interface for R (an integrated development environment, IDE)

Source: Statistical Inference via Data Science

RStudio IDE

Quarto

  • Fully reproducible reports – the analysis is run from the beginning each time you render

  • Code goes in chunks and narrative goes outside of chunks

  • Visual editor to make document editing experience similar to a word processor (Google docs, Word, Pages, etc.)

Quarto

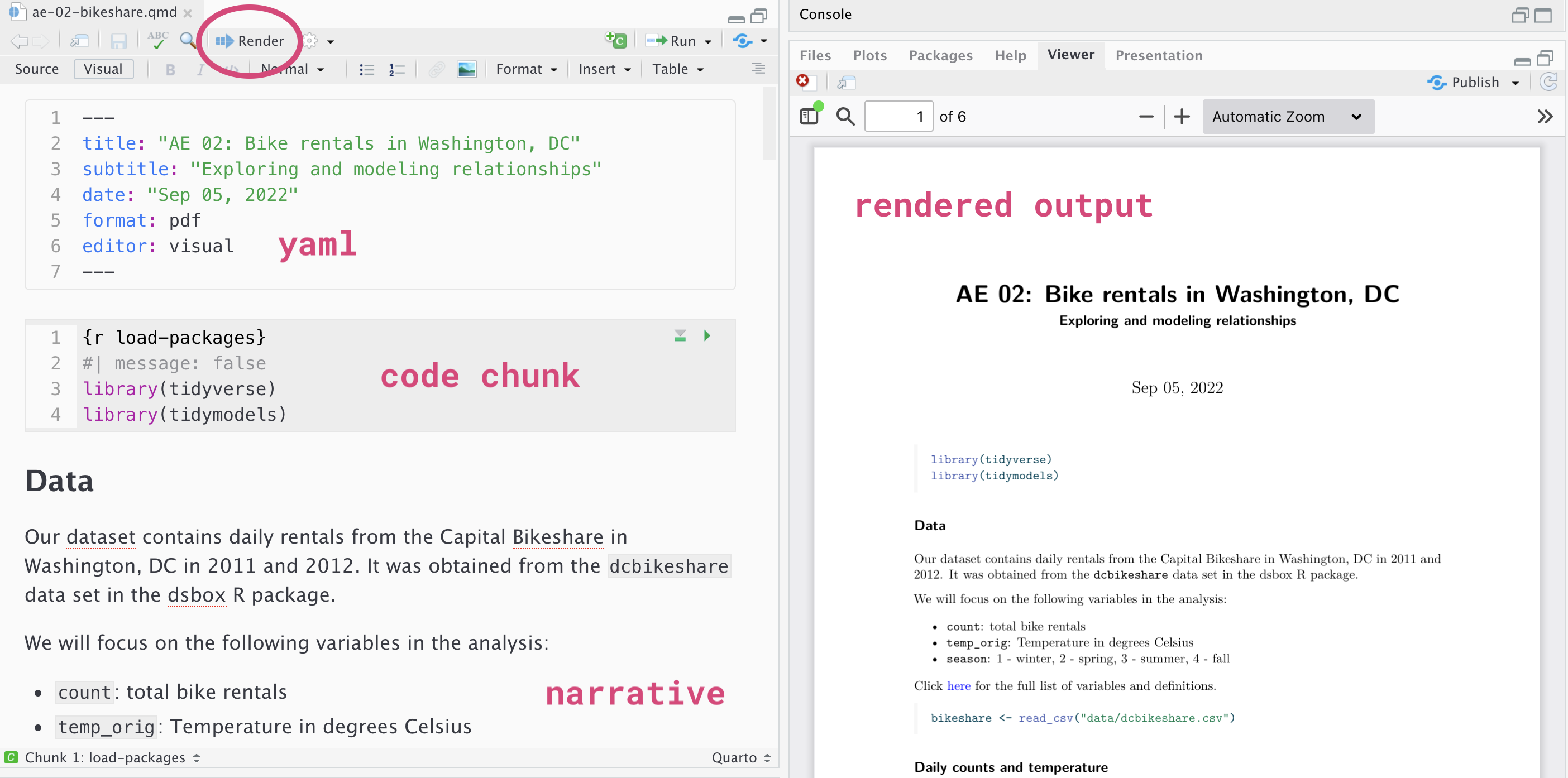
How will we use Quarto?

  • Every application exercise and assignment is written in a Quarto document

  • You’ll have a template Quarto document to start with

  • The amount of scaffolding in the template will decrease over the semester

Version control with git and GitHub

What is versioning?


What is versioning?

with human readable messages

Why do we need version control?

Provides a clear record of how the analysis methods evolved. This makes analysis auditable and thus more trustworthy and reliable. (Ostblom and Timbers 2022)

git and GitHub

  • git is a version control system – like “Track Changes” features from Microsoft Word.
  • GitHub is the home for your git-based projects on the internet (like DropBox but much better).
  • There are a lot of git commands and very few people know them all. 99% of the time you will use git to add, commit, push, and pull.

Multivariable relationships

Carbohydrates in Starbucks food

  • Starbucks often displays the total calories in their food items but not the other nutritional information.

  • Carbohydrates are a body’s main fuel source. The Dietary Guidelines for America recommend that carbohydrates make up 45% to 65% of total daily calories.1

  • Our goal is to understand the relationship between the amount of carbohydrates and calories in Starbucks food items. We’d also like to assess if the relationship differs based on the type of food item (bakery, salad, sandwich, etc.)

Starbucks data

  • Observations: 77 Starbucks food items
  • Variables:
    • carb: Total carbohydrates (in grams)
    • calories: Total calories
    • bakery: 1: bakery food item, 0: other food type

Terminology

  • carb is the response variable
    • variable whose variation we want to understand / variable we wish to predict
    • also known as outcome or dependent variable
  • calories, bakery are the predictor variables
    • variables used to account for variation in the response
    • also known as explanatory, independent, or input variables

Univariate exploratory data analysis

Bivariate exploratory data analysis

Function between response and predictors

\[\text{carb} = f(\text{calories}, \text{bakery}) + \epsilon\]

  • Goal: Determine \(f\)
  • How do we determine \(f\)?
    • Make an assumption about the functional form \(f\) (parametric model)
    • Use the data to fit a model based on that form

Determine \(f\)

  1. Choose the functional form of \(f\), i.e., choose the appropriate model given the response variable
  • Suppose \(f\) takes the form of a linear model
    \[y = f(\mathbf{X}) = \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p + \epsilon\]
  1. Use the data to fit (or train) the model, i.e, estimate the model parameters, \(\beta_0, \beta_1, \ldots, \beta_p\)

Carb vs. Calories

\[\text{carb} = \beta_0 + \beta_1 ~\text{calories} + \epsilon\]

Carb vs. Calories + Bakery

\[\text{carb} = \beta_0 + \beta_1 ~\text{calories} + \beta_2 ~\text{bakery} + \epsilon\]

Carb vs. Calories + Bakery (with interaction)

\[{\small \text{carb} = \beta_0 + \beta_1 ~\text{calories} + \beta_2 ~\text{bakery} + \beta_3 ~ \text{calories} \times \text{bakery} + \epsilon}\]

Statistical model vs. regression equation

Statistical model (also known as data-generating model)

\[{\small \text{carb} = \beta_0 + \beta_1 ~\text{calories} + \beta_2 ~\text{bakery} + \beta_3 ~ \text{calories} \times \text{bakery} + \epsilon}\]

Models the process for generating values of the response in the population (function + error)


Regression equation

Estimate of the function using the sample data

\[{\small \hat{\text{carb}} = \hat{\beta}_0 + \hat{\beta}_1 ~\text{calories} + \hat{\beta}_2 ~\text{bakery} + \hat{\beta}_3 ~ \text{calories} \times \text{bakery}}\]

Why fit a model?

  • Prediction: Expected value of the response variable for given values of the predictor variables

  • Inference: Conclusion about the relationship between the response and predictor variables

  • What is an example of a prediction question that can be answered using the model of carb vs. calories and bakery?

  • What is an example of an inference question that can be answered using the model of carb vs. calories and bakery?

Application exercise

📋 sta210-fa23.netlify.app/ae/ae-02-bikeshare

Recap

  • Reproducibility

    • It is best practice conduct all data analysis in a reproducible way

    • We will implement a reproducible workflow using R, Quarto, and git/GitHub

  • Multivariable relationships

    • We can use exploratory data analysis to describe the relationship between two variables

    • We make an assumption about the relationship between variables when doing linear regression

    • The two main objectives for fitting a linear regression model are (1) prediction and (2) inference

References

🔗 STA 210 - Fall 2023 - Schedule

Alexander, Rohan. 2023. “Telling Stories with Data,” June. https://doi.org/10.1201/9781003229407.
Ostblom, Joel, and Tiffany Timbers. 2022. “Opinionated Practices for Teaching Reproducibility: Motivation, Guided Instruction and Practice.” Journal of Statistics and Data Science Education 30 (3): 241–50. https://doi.org/10.1080/26939169.2022.2074922.